Econ-ML
A repository of papers that bring machine learning into economics and econometrics curated by John Coglianese, William Murdock, Ashesh Rambachan, Jonathan Roth, Elizabeth Santorella, and Jann Spiess
Inherent Trade-Offs in the Fair Determination of Risk Scores
How do we tell if an algorithm is discriminating on the basis of race or other characteristics? Public concern over discriminatory algorithms is high. Books such as Weapons of Math Destruction and Automating Inequality detail the ways algorithms further disadvantage the disadvantaged. New York City’s City Council has passed an algorithmic accountability bill. Barocas and Selbst warn that machine learning algorithms have the potential to “inherit the prejudices of prior decision makers”, “reflect widespread biases,” and discover “preexisting patterns of exclusion and inequality.”
Kleinberg, Mullainathan, and Raghavan show that even without these nefarious factors at play, it is usually impossible for an algorithm to be fair by all of three seemingly sensible definitions. They study the case of risk assessments, which they define as “ways of dividing people up into sets [….] and then assigning each set a probability estimate that the people in this set belong to the positive class.” For concreteness, consider the COMPAS algorithm, a controversial tool that predicts recidivism. the “positive class” is those who do recidivize, and the negative class is those who do not. They define three criteria and show that, any risk assessment algorithm is unfair by at least one of the criteria, unless the algorithm makes perfect predictions or the groups have the same true rate of belonging to the positive class.
The criteria are
(A) Calibration within groups requires that for each group $t$, and each bin $b$ with associated score $\nu_b$, the expected number of people from group $t$ in $b$ who belong to the positive class should be a $\nu_b$ fraction of the expected number of people from group $t$ assigned to $b$.
(B) Balance for the negative class requires that the average score assigned to people of group 1 who belong to the negative class should be the same as the average score assigned to people of group 2 who belong to the negative class. In other words, the assignment of scores shouldn’t be systematically more inaccurate for negative instances in one group than the other.
(C) Balance for the positive class symmetrically requires that the average score assigned to people of group 1 who belong to the positive class should be the same as the average score assigned to people of group 2 who belong to the positive class.
A ProPublica analysis of argued that, based on COMPAS’s rates of false positives and false negatives, it is biased against blacks. Black people who don’t recidivize don’t receive the same average scores as white people who don’t recidivize. That’s failing criteria B and C. Rebuttals such as Dieterich, Mendoza, and Brennan asserted that the algorithm did not exhibit racial bias, since it was well-calibrated in that within each racial group. That’s criterion A: a white person and a black person each assigned a 10% chance of recidivizing by the algorithm each actually have about a 10% chance of recidivizing.
Example
The authors prove mathematically why the criteria generally cannot be simultaneously satisfied. But to gain intuition for how an algorithm can exhibit such behavior, let’s look at a simple example using a test that detects breast cancer, using simulated data. The test is fair in that a man and a woman with the same latent breast cancer risk are treated similarly, but unfair in that it leaves men with breast cancer less likely to receive treatment than women with breast cancer. That is, it obeys Criterion A but violates Criterion C.
First, let’s generate data using Python (with Numpy and Pandas) where everyone is either a man or a woman. Everyone has some latent probability to get breast cancer; in this fake data, 50% of women and 23% of men have breast cancer.
n = int(1e6)
gender = np.random.uniform(0, 1, n) < .5
data = pd.DataFrame({'gender':
pd.Categorical.from_codes(gender,
categories=['female', 'male'])})
cancer_propensity = np.random.normal(-2, 2, n) \
+ 2 * (data['gender'] == 'female')
data['breast cancer probability'] = \
np.exp(cancer_propensity) / (1 + np.exp(cancer_propensity))
data['has breast cancer'] =\
np.random.uniform(0, 1, n) < data['breast cancer probability']
data.head()
| gender | breast cancer probability | has breast cancer | |
|---|---|---|---|
| 0 | male | 0.262918 | False |
| 1 | male | 0.338493 | False |
| 2 | male | 0.204863 | False |
| 3 | female | 0.869441 | True |
| 4 | male | 0.093922 | False |
Let’s say that a machine learning algorithm assigns each person a probability of having breast cancer. Specifically, it assigns them their true “breast cancer probability” in the above data. Let’s put people into score bins, and see if the algorithm that assigned the score was well-calibrated.
data['bin'] = np.round(data['breast cancer probability'].values, 1)
Criterion A: Calibration within groups
Out of women assigned to the 10% bin, about 10% have cancer, and out of those in the 20% bin, about 20% have cancer, and so on. The same holds for men. Therefore, the algorithm is unbiased according to criterion A.
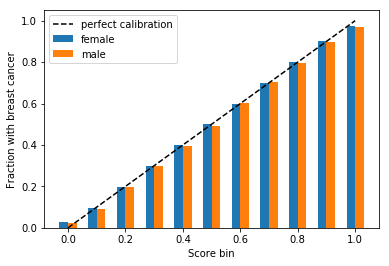
Criterion C: Balance for the positive class
Do men with breast cancer and women with breast cancer have the same scores on average? No, on average men with cancer had lower scores than women with cancer. The average woman with cancer had a score of 69.7, and the average man had a score of 50.1.
Let’s say people with a score greater than .1 are recommended for further treatment. Then 98.6% of women who have breast cancer would be correctly assigned to get further treatment, but only 92.3% of men would. In other words, men with breast cancer are more than five times as likely as women with breast cancer to fail to receive medical treatment. So using a “false negative” test, the algorithm is discriminating against men.
fairness discrimination risk scoring
Reviewed by Elizabeth on .