Econ-ML
A repository of papers that bring machine learning into economics and econometrics curated by John Coglianese, William Murdock, Ashesh Rambachan, Jonathan Roth, Elizabeth Santorella, and Jann Spiess
Data-Driven Tuning, 50 Years Earlier
Willard James and Charles Stein (1960): Estimation with Quadratic Loss. Fourth Berkeley Symposium.
Shrinkage reduces the variance of estimators at the cost of some bias. Whether this regularization improves precision depends on its tuning, i.e. the choice of shrinkage factor. James and Stein show that for the estimation of at least three Normal means there is a data-driven choice of the tuning parameter that always beats the unregularized estimator. The result extends to high-dimensional out-of-sample prediction (Baranchik, 1973).
Highlight:
An explicit expression of the optimal shrinkage factor and the risk of the corresponding estimator:
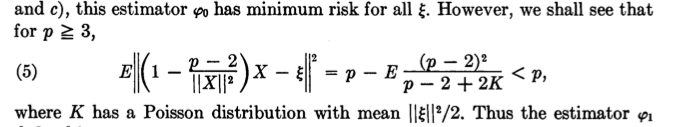
Bonus:
Stein could not get hold of James when submitting the paper. Since he was not sure about Willard James’ first name, the latter is listed simply as “W. James”:
shrinkage beta-hat regularization
Reviewed by Jann on . Suggested by Sendhil.