Econ-ML

Sparsity in Economic Predictions

Domenico Giannone, Michele Lenza, and Giorgio Primiceri (2017): Economic Predictions with Big Data - The Illusion of Sparsity. Working Paper.

Underlying many machine learning prediction techniques is an implicit assumption of sparsity. That is, out of the many potential covariates, machine learning techniques typically assume that only a few are actually relevant for the prediction task at hand. For instance, LASSO leverages the sparsity assumption by setting several coefficients to be exactly zero, thereby performing variable selection. Giannone, Lenza and Primiceri (2017) consider whether sparsity is a reasonable assumption in a variety of economic prediction problems. The authors consider prediction problems in macroeconomics, finance and applied microeconomic such as forecasting economic activity in the US, predicting variation in the US equity premium and forecasting appellate decisions in eminent domain cases. To evaluate the sparsity assumption, Giannone, Lenza and Primiceri (2017) use a spike-slab prior to perform inference on the probability of variable inclusion and the degree of shrinkage conditional on inclusion. They find that, at least in the applications they consider, the posterior probability of variable inclusion tends to be clustered around high values for each available covariate. Moreover, the best set predictors are typically formed by averaging the predictions of several models, each with different sets of included covariates. This suggests that the true data-generating processes are dense, not sparse. As a result, Giannone, Lenza and Primiceri (2017) conclude that there may be the “illusion of sparsity” in many economic prediction problems.

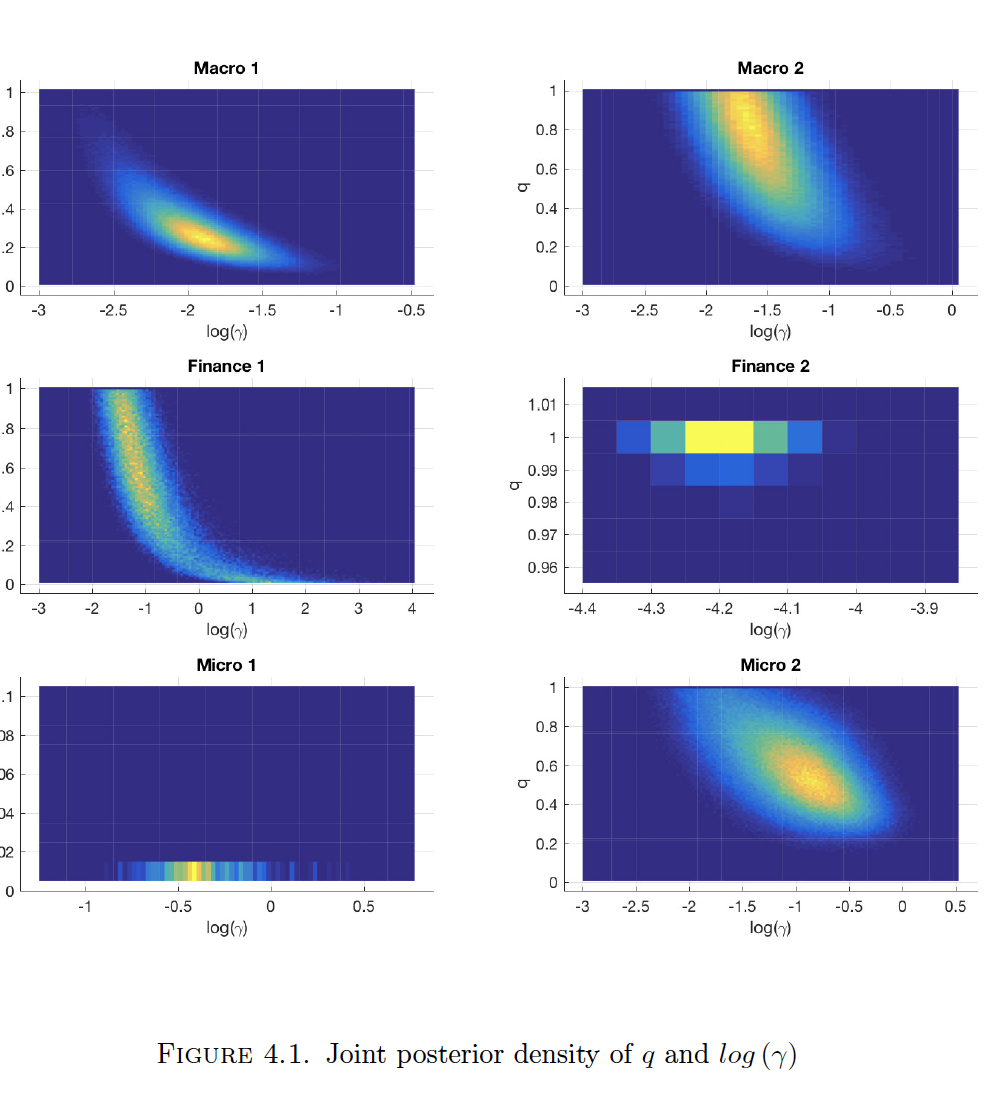
Highlight: The authors construct these beautiful heat plots of the posterior joint density for the two key hyperparameters - q and log(gamma). q controls the probability of inclusion of a covariate and gamma controls the variance of the coefficient on the covariate conditional on inclusion. In the spike and slab prior, a lower variance of the coefficient can be interpreted as more shrinkage. Brighter colors are associated with more probability mass. Aside from the applied micro applications, most mass appears to concentrated on high values of q, suggesting a dense model. Moreover, high values of q are associated with low values of gamma, meaning that denser models typically require more shrinkage. As a result, the authors note variable selection techniques such as LASSO may artificially recover sparse representations even though the data suggest a dense model.

prediction sparsity spike and slab

Reviewed by Ashesh on October 31, 2017.