Econ-ML

The Costs of Algorithmic Fairness

Sam Corbett-Davies, Sanjog Misra, Emma Pierson, Avi Feller, Sharad Goel, and Aziz Huq (2017): Algorithmic decision making and the cost of fairness. ArXiv.

Society is increasingly relying on algorithms to make decisions in areas as diverse as the criminal justice system and healthcare, but concerns abound about whether algorithmic decision-making may induce racial or gender bias. This paper formalizes three notions of algorithmic fairness as constraints on the decision rule, and shows what the optimal decision rule looks like subject to these constraints. The authors then apply these rules to the context of bail decisions, and estimate the costs of imposing different notions of algorithmic fairness in terms of the number of additional crimes committed relative to an unrestrained decision rule.

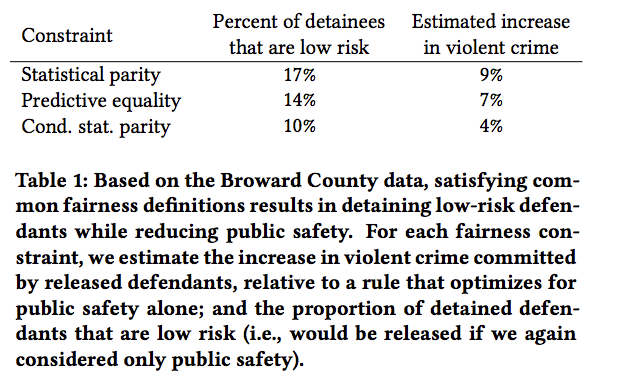
The authors formalize three notions of algorithmic fairness for an algorithm that makes a binary decision (e.g. release on bail) given covariates about an individual. Statistical parity is the notion that the probability the action is taken is the same across groups; conditional statistical parity is the notion that the probability the action is taken is the same across groups, conditional on certain permitted characteristics (e.g. previous arrests); and finally, predictive equality is the notion that the false positive rate should be the same across groups. The authors show that the optimal decision rule that achieves each of these constraints can be written as a threshold rule in the predicted risk score, where the thresholds potentially differ by race. They then turn to the decision of whether a defendant should be released on bail, and estimate the optimal decision rule subject to each fairness constraint using data from Broward County, Florida. They find that imposing statistical parity would increase violate crimes by 9% relative to the unconstrained algorithm, but would substantially reduce racial inequality – the unconstrained rule detains 40% of blacks and only 18% of whites. Finally, they show that even if blacks and whites have the same risk on average, a decision rule may have different impacts by race if the distribution of predicted risk conditional on covariates varies by race.

Highlight: Using crime data from Broward County, they estimate the increase in crime that would result if various notions of algorithmic fairness were imposed on the decision of whether to release an arrestee on bail; all decision rules are required to retain only 30 percent of defendants.

algorithmic fairness algorithmic decision making

Reviewed by Jon on December 10, 2017.